The average gasoline price per gallon (in cities) and the cost of a barrel of oil are shown for a random selection of weeks in 2015. Is there sufficient evidence to conclude a strong linear relationship between the variables, with a significance of \(\alpha=0.05\)?

Oil ($)	51.91	60.65	59.56	52.86	45.12	44.21
Gasoline ($)	1.97	1.96	2.06	2.04	2.00	1.99

Step 1:

We count the number of pairs. We see that we have chosen 6 weeks.

Step 2: 

We enter our data into the correlation calculator.

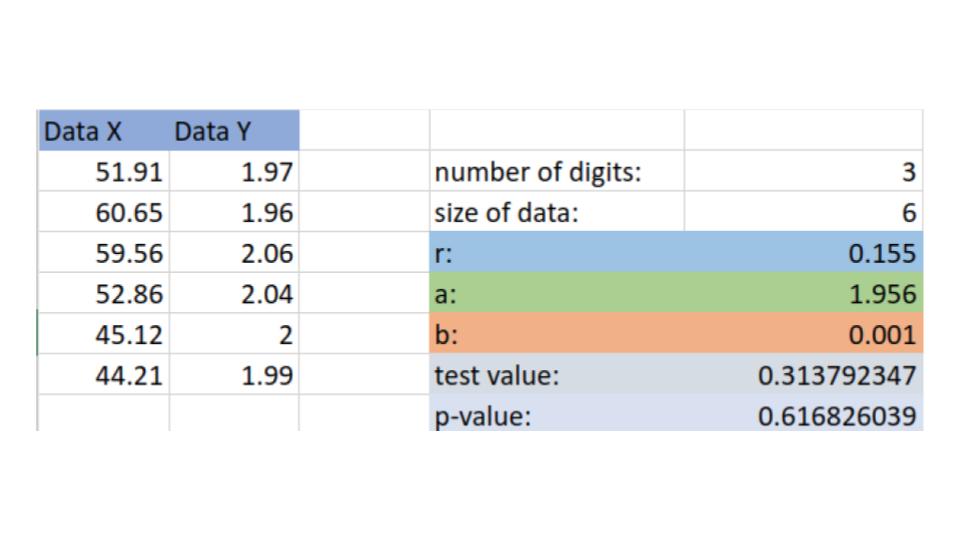
We see that we get a p-value of 0.6168, i.e. when we assume our null hypothesis (that \(\rho=0\) that there is no linear relationship, we had approximately a 62% chance of choosing a sample with a smaller correlation score.

Step 3:

Conclusion.

Since our alternative hypothesis is \(\rho\neq0\) we are doing a two-tailed test, we see that:

\[\frac{\alpha}{2}<p=0.6168<\left(1-\frac{\alpha}{2}\right)\]

we do not reject \(H_0\) and thus we do not have enough evidence to suggest their is a strong linear relationship.